Optical fibers, a major contributor to the $7 trillion annual global economic impact of light, enable all modern means of communication—from streaming videos and telemedicine to bank transfers and e-commerce. They also are used in medical endoscopes to peer into the body and to bring high-power laser light to machine parts used in practically all modern electronics, automobiles, and planes. In bestowing the 2009 Nobel Prize in Physics to Charles Kao for “groundbreaking achievements concerning the transmission of light in fibers for optical communication,” the Nobel Committee validated the global impact and societal benefits of optical fiber.
Optical fibers are hair-thin strands of ultra-pure glass, consisting of a central core (with a diameter on the order of 10 µm) surrounded by cladding (with a diameter of 125 µm for telecommunications fibers). The light on which information is encoded is confined to the central core region, whose refractive index, a relative measure of the speed of light, is slightly higher than that of the surrounding cladding.
If one were able to couple all of the light from a typical red laser pointer (5 mW) into the core of an optical fiber, the intensity of light (power/area) would be on the order of 64 MW/m2. To put this into perspective, the intensity of the Sun’s light on the surface of the Earth is about 1,000 W/m2.
Accordingly, the intensity of light from a laser pointer focused into the core of a conventional optical fiber is about 64,000 times brighter than the intensity we see sitting on a beach. Now imagine a directed energy defense system operating at 1 kW of laser power rather than a 5 mW laser pointer—at some point, the glass cries “Uncle!”
Glass’s capitulation to light results in a cornucopia of effects. At low intensity levels, optical fiber behaves like a small window, where light enters, passes through, and leaves without much interaction (i.e., loss of intensity). Now with increasing intensity, however, the color of light or its range of colors is converted through numerous nonlinear phenomena. While interesting and, in a few cases, useful in their own right, such nonlinearities generally are considered parasitic to performance and are undesirable.
Optical nonlinearities that limit the performance of modern optical fibers, and lasers made from said fibers, include stimulated Brillouin scattering, stimulated Raman scattering, and nonlinear refractive index (n2)-related wave-mixing phenomena. Since these parasitic nonlinearities arise at high intensities, the fiber community has largely managed these issues by designing fibers that spread light propagating in the core over a larger cross-sectional area—called “large effective area” fibers.
For a given power level (W), a larger effective area (m2) reduces the effective intensity (W/m2), ideally keeping it below a critical threshold value. However, as power levels have continued to increase, the requisite mode areas have had to concomitantly grow, inducing additional parasitic effects. The primary example is transverse mode instability (TMI), a thermally-driven process where distribution of light in the large core randomizes and becomes dynamic above a certain threshold. Indeed, TMI is presently the dominant limitation in power-scaling of fiber-based, high-power lasers.1
Absent from this discussion so far has been any comment on the nature of the glass from which the fiber is composed. The vast majority of commercial optical fibers are high SiO2-content silicates and are fabricated by vapor-deposition methods. These methods were developed more than 40 years ago and have enabled the ubiquitous optical fibers of today. The choice of silica and its resulting high strength, low loss, and massive production scale fibers result from the process itself.1
Today’s optical fibers are made from the same high-silica content compositions as they have for decades, and their optical performance is engineered “geometrically.” While such microstructuring does afford novel effects and enhanced performance, it also increases cost and lowers yield.
An alternative approach to manage parasitic optical nonlinearities is to keep the fiber simple and instead engineer the glass from which it is made. It is the interaction of light with the material that fundamentally originates nonlinearities in the first place—so why not attack the problem at its source? Indeed, in a recent series of papers, we have advocated such a “unified materials” approach.2–5
A unified materials approach to mitigate optical nonlinearities
While aiming to “attack the problem at its source” sounds somewhat intuitive, there are two additional, though less obvious, benefits. By tailoring glass composition and structure to influence its interaction with light, a materials approach directly attacks spontaneous scattering—i.e., initial stages of the progression or “turn-on” of nonlinear parasitics.
First, since practical problems arise from stimulated scattering, reducing spontaneous scattering before the process can become stimulated is that much more effective. Second, glass compositional tailoring can impact several nonlinearities simultaneously, since composition and structure modify multiple physical, optical, and acoustic properties.
With this in mind, a brief description of the material factors that influence the aforementioned performance-limiting parasitic effects follow. Figure 1 provides a summary of these nonlinearities and their origins, impact, and material dependencies.

Figure 1. Summary of parasitic optical nonlinearities plaguing modern optical fibers. Credit: John Ballato
Brillouin scattering
Brillouin scattering is a coupling between the glass’s acoustic phonons and the light. In its spontaneous form, Brillouin scattering is materially proportional to n8 p212KS, where n is refractive index, p12 is transverse photoelastic (Pockels) coefficient, and KS is adiabatic compressibility of the glass through which the light is propagating.
Above a threshold power level—which has been known for more than 40 years to be as low as tens of milliwatts in low-loss fibers6—the spontaneous effect becomes stimulated. In its stimulated form, the Brillouin gain coefficient (BGC) is proportional to n7 p212/ ρVa ΔνB, where ρ is density, Va is acoustic velocity, and ∆νB is Brillouin linewidth. This stimulated scattering acts as a highly efficient (back) reflector to the light that can severely damage the optical system and limits the power per unit bandwidth that can be coupled into, or produced from, an optical fiber.
In the particular case of reducing Brillouin scattering, the most powerful approach is to materially attack the problem through p12 photoelasticity. This is because it is the only relevant property that can take on a value of zero, which would completely eradicate Brillouin scattering. In theory, this can be achieved through compositional additivity of a positive p12 material, such as SiO2 (p12 = 0.226), with a negative p12 component, such as BaO, SrO, or Al2O3. However, to date, glass formation remains elusive in these systems.
That said, aluminosilicate glasses have achieved quite remarkable and practical 100-fold reductions in BGC relative to conventional silica optical fibers.7 Ternary systems, particularly based on alkaline earth aluminosilicates (e.g., SrO–Al2O3–SiO2), have even greater promise for completely removing Brillouin scattering as a parasitic limitation in high-power and high-energy laser systems.5
Raman scattering
Raman scattering also is an acousto-optic interaction but involves creation (Stokes’) or annihilation (anti-Stokes’) of optical phonons in glass (e.g., excitation of Si-O-Si vibrational modes in silica glass) and light. Such phenomena can be problematic when wavelength control is mandatory.
From a materials perspective, spontaneous Raman scattering is proportional to the molar volume and the square of the bond compressibility parameter. Qualitatively then, Raman scattering (both spontaneous and stimulated forms) is reduced for glasses that possess a low molar volume and small bond compressibility parameter.
In practice, this is somewhat easier said than done, so a more straightforward approach to intrinsically low Raman scattering is a more highly disordered glass structure (which broadens the Raman spectrum), high concentrations of low Raman gain coefficient constituents, and components with minimal overlap in their respective Raman spectra. Using this materials approach, for example, yttrium aluminosilicate glass fibers have been realized that exhibit one-half the Raman scattering of conventional SiO2.8
Transverse mode instabilities
TMI is thermally driven mode-hopping associated with dynamic spatial heat fluctuations in a fiber. TMI is due to stimulated thermal Rayleigh scattering and arises when an index grating is formed that phase-matches propagating modes of the incident and scattered light in a multimode (large mode area) optical fiber that is lasing above a given threshold power.
By materially attacking TMI through the thermo-optic coefficient (TOC), one lessens thermo-optic (dn/dT) changes in the fiber as it heats up under lasing. Interestingly, though not related to stimulated thermal Rayleigh scattering, another line of attack is to generate less heat in the first place.
Materially, TMI is proportional to TOC/(ρ×Cp), where ρ is density and Cp is specific heat.2 Of these properties, TOC offers greater compositional tailorability and, as with Brillouin scattering, has the potential to take on a zero value when using materials with positive (e.g., SiO2, Al2O3) and negative (e.g., BaF2, SrF2) TOC values. Recently, an alkaline earth alumino-fluorosilicate in the SrF2–Al2O3–SiO2 system exhibited a two-fold reduction in TOC.9
A laser heats up during operation either because impurities absorb some of the light (pump or signal) or because transitions that yield the light are not perfectly efficient. Such nonradiative relaxations indeed are a major source of heat generation in vapor-deposited silica-based fiber lasers. The ratio of the pump-to-signal wavelength is proportional to the “quantum defect” (QD). Since glass composition can influence the absorption and emission spectra of (rare earth-doped) active glasses, QD tailoring is another materials-related approach to reduce nonlinearities.
In the case of the aforementioned fluorosilicate, fluorine blue-shifts the ytterbium emission peak in comparison to conventional ytterbium-doped aluminosilicate laser fibers, resulting in a potential QD of <1%—as opposed to the typical 5% with conventional fibers—while preserving high slope efficiencies.9 A reduced QD permits lasing that emits lower energy phonons, leading to less heat generation, better thermal management, and lower parasitic thermo-optical effects.
n2-wave-mixing phenomena
In addition to Brillouin and Raman scattering, the nonlinear component of the refractive index (n2) is parasitic in that it enables wave-mixing phenomena above a critical threshold power. In such cases, the refractive index is spatially and temporally modulated and results in spectral broadening of the optical signal. Other n2-related effects, such as self-focusing, can also irreversibly damage the fiber.
Suppressing these wave-mixing nonlinearities materially requires a reduction of n2. However, in practice, silica already exhibits an impressively low n2 value. Most efforts to tailor the magnitude of n2 have relied on fluorine and phosphorus doping of SiO2. In the former case, lower polarization of the fluorine ion relative to oxygen reduces n2. In the latter case, higher valence state of the phosphorous ion relative to the silicon ion promotes greater covalency, thereby reducing polarization.
Here again, the SrF2–Al2O3–SiO2 system is of interest—while it exhibits n2 values that are similar to silica, this is surprising given that both strontium and aluminum increase n2, while fluorine decreases it, relative to SiO2.9
Glass composition additivity modeling
While a materials approach to mitigate optical nonlinearities is highly effective, the compositional space over which fibers can be made is considerable, if not entirely daunting. Accordingly, property modeling is especially necessary.
That said, there are a great variety of glass structure–property models of varying sophistication and computational intensity. For reasons of speed, relative simplicity, and surprising accuracy, we have opted for the century-old additivity model of Winklemann and Schott, with suitable improvements and extensions to other material properties relevant to modern optical fibers.3–5
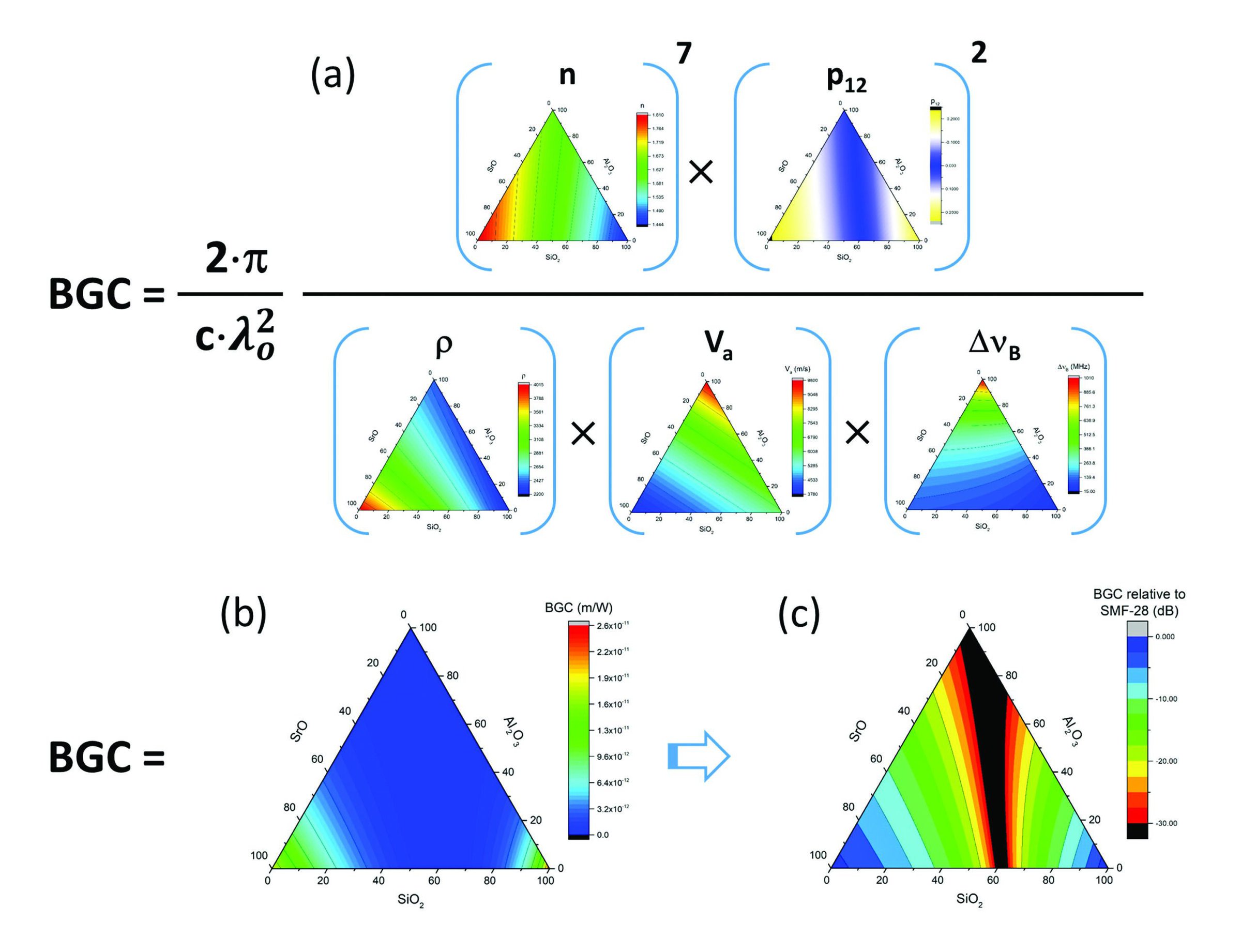
Figure 2. Graphical representation of compositional dependence of the Brillouin gain coefficient (BGC) in a ternary SrO–Al2O3–SiO2 system. (a) BGC equation overlaid with triaxial diagrams for each material property computed within the entire ternary system. (b) Resultant computed BGC (m/W) for the ternary system. (c) BGC for the SrO–Al2O3–SiO2 system relative to that for conventional single-mode fiber (SMF-28). The black region denotes compositions where BGC is suppressed by more than 30 dB relative to conventional fibers. Credit: John Ballato
Figure 2 provides a graphic representation of this approach for the specific case of the BGC, where c is speed of ρ, VA, and ∆νB are defined previously. For further identification of compositional regions of interest, it is useful to normalize these values to those for conventional optical fibers (Figure 2c).
However, not all compositions are glass-forming, so care must be given in how liberally the results are considered. That said, the approach is straightforward and provides a quick and powerful filter for subsequent experimentation.
An old approach to fiberizing old glasses
As noted and expected, not all compositions identified in the property value ternaries form glasses of sufficient stability to be drawn into optical fiber. For example, with respect to aluminosilicates, conventional vapor deposition methods are limited to about 8 mole percent Al2O3 into SiO2.2
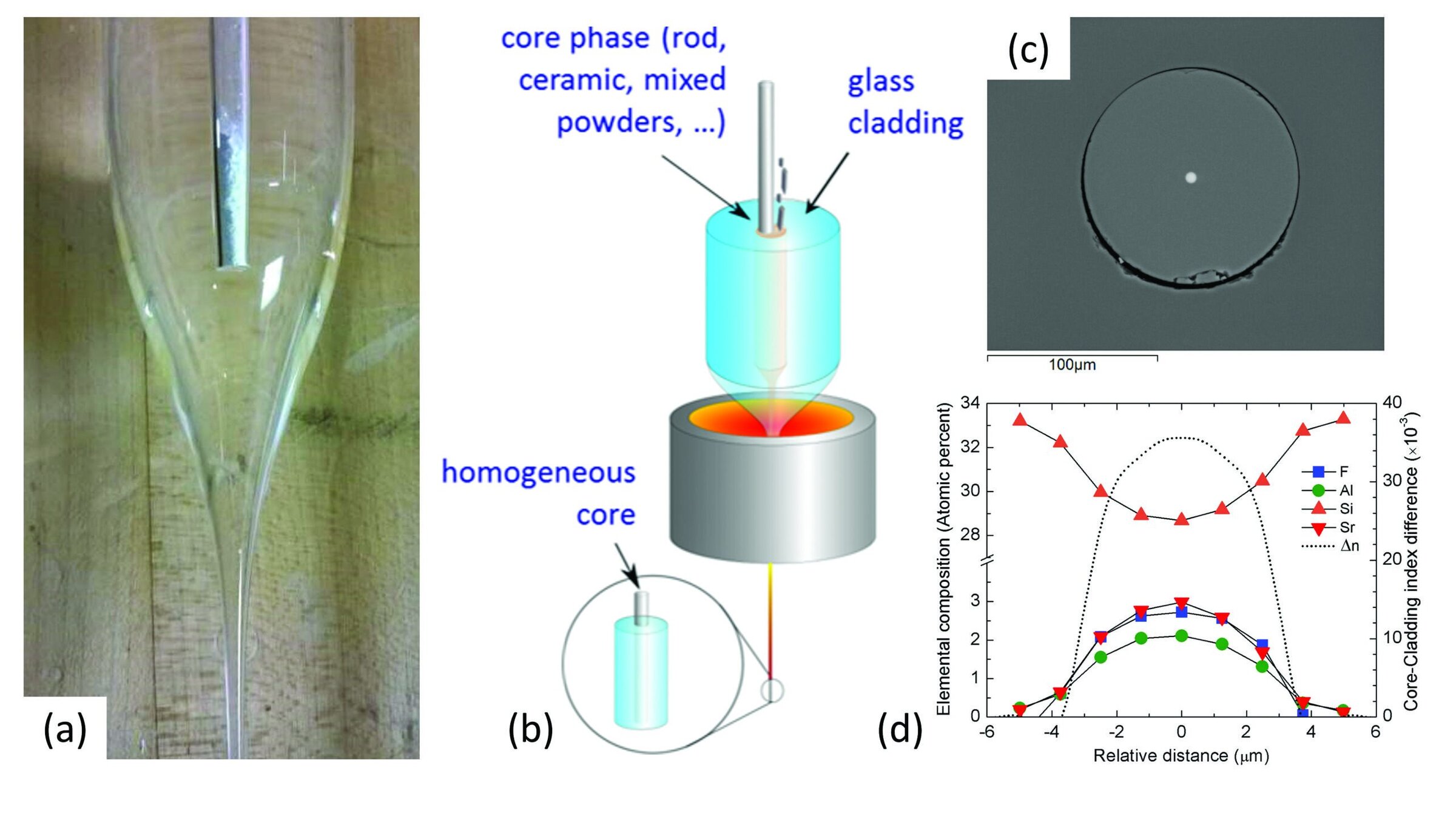
Figure 3. a) Precursor powder mixture inserted inside an optical grade silica capillary preform (3 mm and 30 mm inner and outer diameters, respectively). b) Illustration of the molten core technique. c) Scanning electron micrograph of a circular core-cladding optical fiber. d) Compositional and refractive index profile across the SrF2–Al2O3–SiO2 fiber shown in (c). Not shown for reasons of clarity is oxygen concentration, %O, which can be calculated: %O (At. %) = 100 – [%F + %Sr + %Al + %Si]. Credit: John Ballato
Thus, as the fiber is drawn, the molten liquid core transitions from preform to fiber and is quenched rapidly (>2,000 K/s) as the fiber cools. The core is kinetically trapped in a glassy state (Figure 3c) that is composed of silica from the cladding that dissolves in during the draw, along with precursor components, typically exemplifying a transversally graded index profile (Figure 3d). Species from the cladding glass can dissolve into the core melt during fiber draw, resulting in compositional changes between the starting precursor and resultant fiber.
This section is titled as such because the original molten core fiber approach is now 25 years old.10 It has been used to realize optical fibers with compositions that have themselves been known for more than 100 years in bulk form, although not in fiber form because conventional methods restrict the composition.
In addition to this considerable glass-forming flexibility, the molten core method is also a relatively low-temperature fabrication method because it relies on fiber-drawing temperature (~2,000°C) as opposed to collapse temperature of conventional vapor deposition preform approaches (~2,400°C). This permits greater inclusion of volatile species that otherwise would evaporate.
The “perfect” optical fiber (?)
Each optical nonlinearity that limits current fiber-based laser systems can be dramatically reduced, if not entirely negated, through judicious selection of appropriate glass compositions. In the section above, each parasitic phenomenon was treated individually. However, they possess many of the same enabling materials properties, so a natural question is “can one composition minimize all nonlinearities?” Indeed this is the question that we set out to answer in our previous publications.2–5,11
The simple answer is: maybe.
While compositions do exist where, for example, Brillouin scattering and stimulated thermal Rayleigh scattering can reach zero (e.g., p12 and TOC = 0), these compositions are unstable against crystallization. Thus in practice, reductions on the order of even 50% are useful.
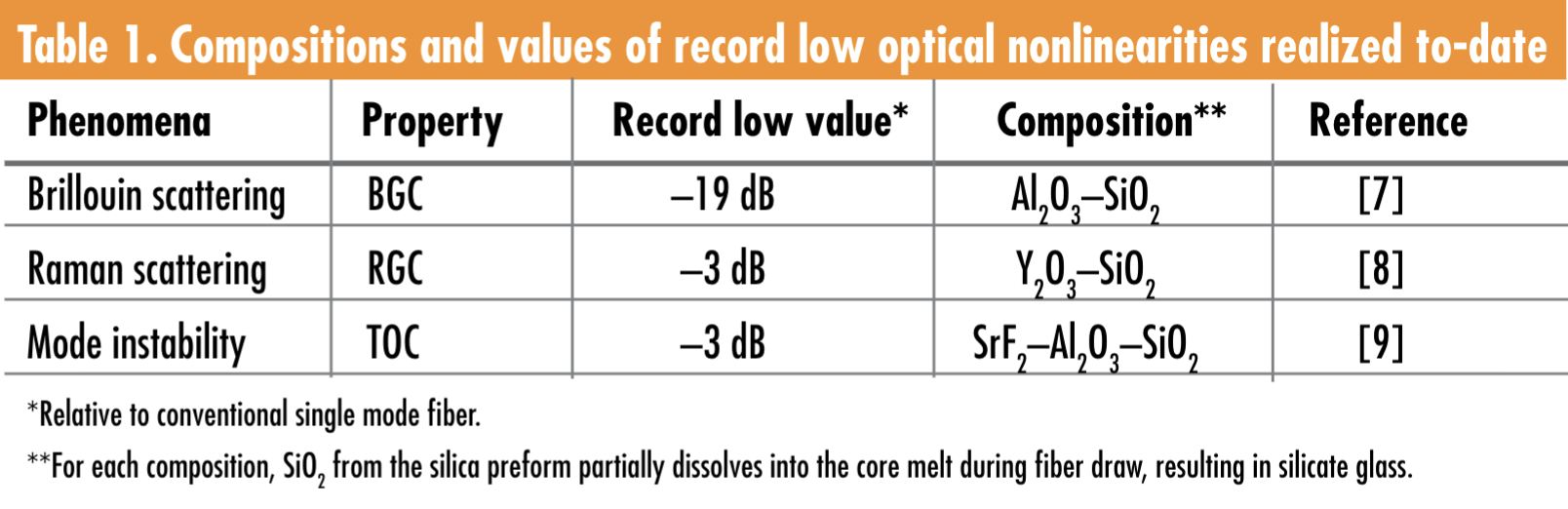
Table 1 provides record published values to date for individual nonlinearities.7–9 The best “unified” values achieved to date from a single glass fiber, relative to conventional single-mode fiber, are about –7.9 dB in BGC, –1.6 dB in RGC, and –3.1 dB in TOC (fiber designated “YbF-SrAlSiF” in Cavillon et al.9).
Future efforts
We highlight a new approach to manage performance-limiting effects in modern optical fibers. Rather than control light through the fiber’s geometric design, we describe an enabling materials approach that attacks parasitic nonlinearities at their fundamental origin: the light–matter interaction.
Through judicious selection of glass composition, such optical nonlinearities cannot only be reduced, but may even be wholly negated. This would not only obviate existing limitations, but also open up entirely new light-based defense, security, medical, and manufacturing opportunities.
The two most paramount targeted opportunities for future efforts are glass formation and attenuation. With respect to glass formation, as noted, the compositions of greatest interest in truly mitigating optical nonlinearities cannot be made using conventional vapor-deposition methods. Similarly, molten core or powder sintering approaches have not been able to achieve stable glasses with <70 mole percent SiO2 that can be formed into long optical fibers. Novel methods or improvements to existing techniques that permit realization of these intrinsically low nonlinearity compositions in fiber form are needed.
With respect to attenuation, the best molten core-derived fibers fabricated to date exhibit loss values on the order of 150 dB/km, with most prototypes currently in the 1,000 dB/km range. While this is acceptable for property measurement, such values are too high for practical use in most laser systems. Efforts to reduce losses to <50 dB/km would be well worth the effort.
Finally, we hope that this work—which complements our previous publications2–5,8—serves as a call-to-arms for both the glass and fiber optics communities. In the glass community, structure–property–processing expertise is as enabling now as it was 40 years ago, when some of the most seminal advancements in optical fiber originated. In the optical fiber community, although silica and vapor-deposition have made great strides, they are insufficient to truly address present and future performance limitations.
Microstructured optical fibers have their place and do enable some useful properties and intriguing physics. However, their complexity and cost will remain problematic. Indeed, a re-unification of glass and optical fiber fields could provide staggering benefits to industry and society alike.
Acknowledgements
Aspects of this work were financially supported by U.S. Air Force Office of Scientific Research through grant FA9550-16-1-0383 and by the U.S. Department of Defense High Energy Laser Joint Technology Office through grant N00014-17-1-2546. The J.E. Sirrine Foundation also provided financial support (to J.B. and M.C.).
Capsule summary
Guiding light
Optical fibers—hair-thin strands of ultra-pure glass—carry the light that enables diverse applications, such as streaming videos, telemedicine, bank transfers, e-commerce, medical endoscopy, and laser light for machining. Through these myriad applications, optical fibers offer rich global impact and societal benefits.
Approaching limits
The performance of current glass fibers, however, is approaching limits in terms of information and laser power. This is a result of parasitic optical nonlinearities that now, given the ever growing bandwidth and power demands of communications, manufacturing, and defense systems, are no longer inconsequential.
Glass solutions
A new approach to optical fiber engineering and design uses materials to attack parasitic nonlinearities at their fundamental origin: the light–matter interaction. New glass compositions can not only obviate existing limitations, but also open up entirely new light-based defense, security, medical, and manufacturing opportunities.
Cite this article
J. Ballato, M. Cavillon, and P. Dragic, “Guiding light—how new materials are shaping the future of advanced optical fiber and laser systems,” Am. Ceram. Soc. Bull. 2018, 97(4): 22–27.
About the Author(s)
John Ballato and Maxime Cavillon are in the Department of Materials Science and Engineering at Clemson University (Clemson, S.C.). Peter Dragic is in the Department of Electrical and Computer Engineering at the University of Illinois at Urbana-Champaign (Urbana, Ill.). Contact Ballato at jballat@clemson.edu.
Issue
Category
- Electronics
- Glass and optical materials
Article References
1J. Ballato, P.D. Dragic, “Glass: The carrier of light—A brief history of optical fiber,” Int. J. Appl. Glass Sci. 7, 413–422 (2016).
2J. Ballato, M. Cavillon, P.D. Dragic, “A unified materials approach to mitigating optical nonlinearities in optical fiber. I. Thermodynamics of optical scattering,” Int. J. Appl. Glas. Sci., 9, 263–277 (2018).
3P.D. Dragic, M. Cavillon, A. Ballato, J. Ballato, “A unified materials approach to mitigating optical nonlinearities in optical fiber. II. A. Material additivity models and basic glass properties,” Int. J. Appl. Glas. Sci., 9, 278–287 (2018).
4P.D. Dragic, M. Cavillon, A. Ballato, J. Ballato, “A unified materials approach to mitigating optical nonlinearities in optical fiber. II. B. The optical fiber, material additivity and the nonlinear coefficients,” Int. J. Appl. Glas. Sci., in press (2018). DOI: 10.1111/ijag.12329.
5M. Cavillon, C. Kucera, T. Hawkins, J. Dawson, P.D. Dragic, and J. Ballato, “A unified materials approach to mitigating optical nonlinearities in optical fiber. III. Canonical examples and materials road map,” Int. J. Appl. Glas. Sci., in press (2018). DOI 10.1111/ijag.12336.
6R.G. Smith “Optical power handling capacity of low loss optical fibers as determined by stimulated Raman and Brillouin scattering,” Appl. Opt. 11, 2489–2494 (1972).
7P. Dragic, T. Hawkins, S. Morris, J. Ballato, “Sapphire-derived all-glass optical fibers,” Nat. Photonics, 6, 627–633 (2012).
8P.D. Dragic, J. Ballato, “Characterization of the Raman gain spectra in Yb:YAG-derived optical fibers,” Electron. Lett., 49, 895–897 (2013).
9M. Cavillon, C. Kucera, T.W. Hawkins, P.D. Dragic, J. Ballato, “Ytterbium-doped multicomponent fluorosilicate optical fibers with intrinsically low optical nonlinearities,” Opt. Mater. Express, 8, 744–760 (2018).
10J. Ballato, E. Snitzer, “Fabrication of fibers with high rare-earth concentrations for Faraday isolator applications,” Appl. Opt., 34, 6848–6854 (1995).
11J. Ballato, P.D. Dragic, “Rethinking optical fiber: New demands, old glasses,” J. Am. Ceram. Soc., 96, 2675–2692 (2013).
Related Articles
Market Insights
Engineered ceramics support the past, present, and future of aerospace ambitions
Engineered ceramics play key roles in aerospace applications, from structural components to protective coatings that can withstand the high-temperature, reactive environments. Perhaps the earliest success of ceramics in aerospace applications was the use of yttria-stabilized zirconia (YSZ) as thermal barrier coatings (TBCs) on nickel-based superalloys for turbine engine applications. These…
Market Insights
Aerospace ceramics: Global markets to 2029
The global market for aerospace ceramics was valued at $5.3 billion in 2023 and is expected to grow at a compound annual growth rate (CAGR) of 8.0% to reach $8.2 billion by the end of 2029. According to the International Energy Agency, the aviation industry was responsible for 2.5% of…
Market Insights
Innovations in access and technology secure clean water around the world
Food, water, and shelter—the basic necessities of life—are scarce for millions of people around the world. Yet even when these resources are technically obtainable, they may not be available in a format that supports healthy living. Approximately 115 million people worldwide depend on untreated surface water for their daily needs,…




