Stretched exponential relaxation of glasses: Origin of the mixed-alkali effect

As nonequilibrium materials, glasses continuously relax toward the supercooled liquid metastable equilibrium state.^1,2 Although the myth of flowing glasses in cathedrals suggests otherwise,³ the dramatic increase of glass viscosity with decreasing temperature renders relaxation effectively “frozen” at ambient temperature. However, specific glass compositions can surprisingly deform over time, even at low temperature. This phenomenon is known as the thermometer effect^1,4 and is usually attributed to the mixed-alkali effect, which occurs in oxide glasses comprising at least two alkali oxides, AO₂ and BO₂, and manifests as a nonlinear evolution of properties with respect to the fraction A/(A + B).

Despite its practical importance,⁵ we continue to poorly understand the nature of relaxation in the glassy state. To date, no clear atomistic mechanism of structural and stress relaxation is available, which seriously limits our ability to predict and control behavior.⁶ This knowledge gap becomes even more problematic as the need for large screens with higher resolution (smaller pixel size) results in lower tolerances for relaxation and novel LCD fabrication processes (e.g., p-Si applications) require use of higher processing temperatures, further enhancing relaxation.⁵ Addressing these grand challenges⁷ requires a better understanding of the fundamentals of glass relaxation.

Accelerated relaxation technique

To investigate the mixed-alkali effect in glass relaxation, we simulated a series of (K₂O)_x(Na₂O)_16–x(SiO₂)₈₄ (mol%) mixed-alkali silicate glasses, made of 2,991 atoms, with varying x (x = 0–16). We performed molecular dynamics simulations using the well-established Teter potential^8–10 with an integration timestep of 1 fs. We evaluated Coulomb interactions using the Ewald summation method with a cutoff of 12 Å and chose a short-range interaction cutoff of 8.0 Å.

We generated liquids by placing atoms randomly in a simulation box. We then equilibrated liquids at 5,000 K in the isothermal–isobaric (NPT) ensemble (where the number of atoms (N), pressure (P), and temperature (T) are conserved) for 1 ns, at zero pressure, to ensure loss of the memory of initial configuration. We formed glasses by linear cooling of liquids from 5,000 to 0 K, with a cooling rate of 1 K/ps in the NPT ensemble at zero pressure.

To simulate long-term relaxation of these glasses, we relied on an accelerated simulation technique that we recently developed to understand the origin of room-temperature relaxation in Corning Gorilla Glass.^1,4 In that method, simulated glass is subjected to small, cyclic perturbations of volumetric stress. This method mimics the relaxation observed in granular materials subjected to vibrations,¹¹ wherein small vibrations tend to densify the material (artificial aging) and large vibrations randomize grain arrangements (rejuvenation).

Researchers have applied similar ideas relying on the energy landscape approach¹² to noncrystalline solids based on the fact that small stresses deform the energy landscape locally explored by atoms. This can remove some energy barriers that exist at zero stress, thus allowing the system to jump over barriers to relax to lower energy states. Yu et al. provide more details about this method.¹

As expected, stress perturbations allow all glasses to relax toward lower energy states.¹ All glasses tested here showed a gradual compaction in volume upon relaxation (Figure 1). Remarkably, the volume relaxation observed herein followed a stretched exponential decay function that is similar to that observed experimentally.⁴ Further, the mixed (K₂O)₈(Na₂O)₈(SiO₂)₈₄ glass featured a larger densification than binary sodium and potassium silicate glasses. This is a clear demonstration that the thermometer effect is indeed a manifestation of the mixed-alkali effect.

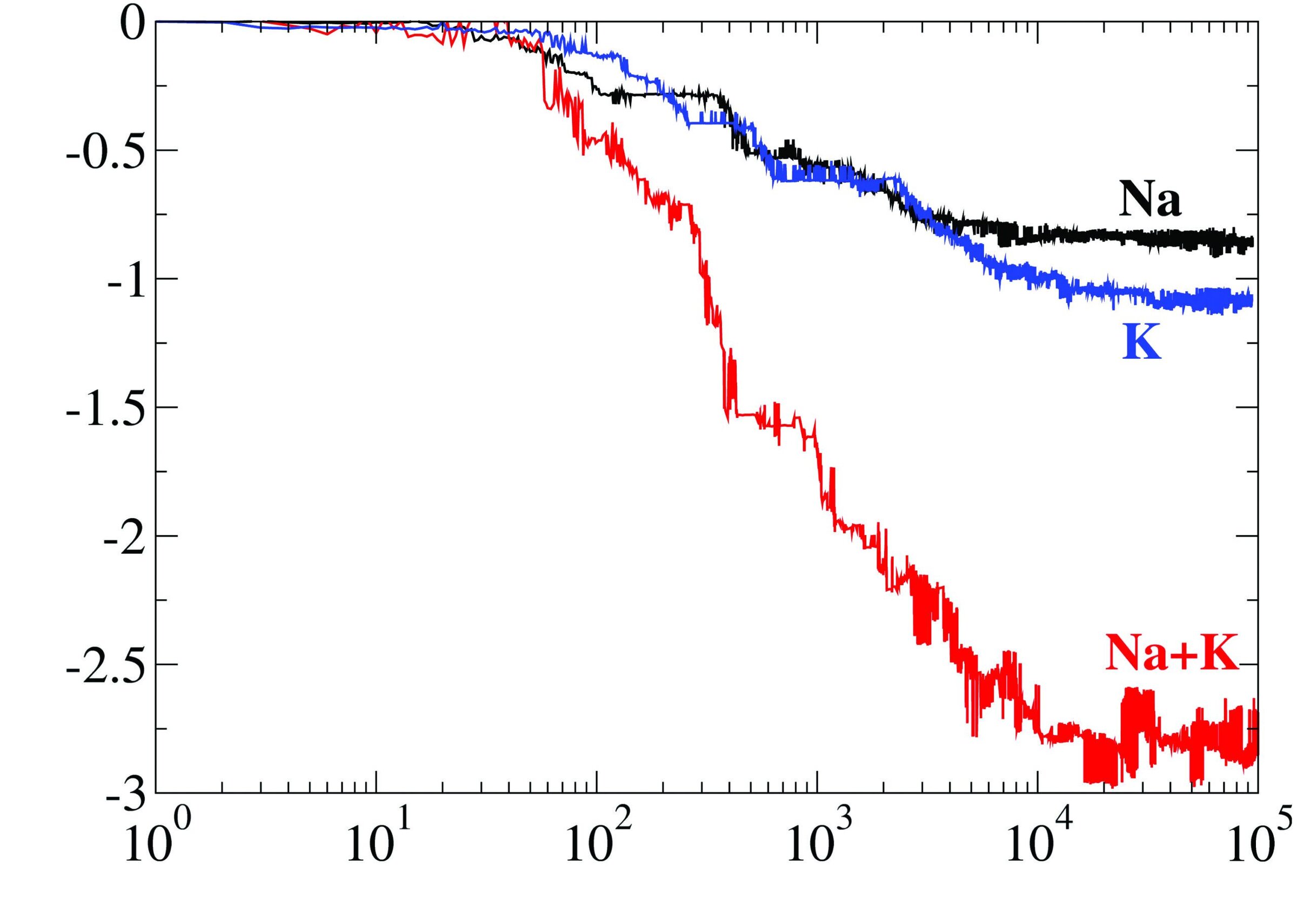
Figure 1. Relative variation of the volume of sodium, potassium, and mixed-alkali silicate glasses with respect to the number of stress perturbation cycles applied. Credit: Yingtian Yu

Origin of the mixed-alkali effect in relaxation

We also investigated the origin of the mixed-alkali effect in the context of relaxation. We can predict the stretched exponential nature of glass relaxation using the Phillips diffusion-trap model, wherein “excitations” in the glass diffuse toward randomly distributed “traps.”¹³ However, this model remains largely axiomatic. Here, we propose that excitations introduced within the diffusion-trap model correspond to locally unstable atomic units.

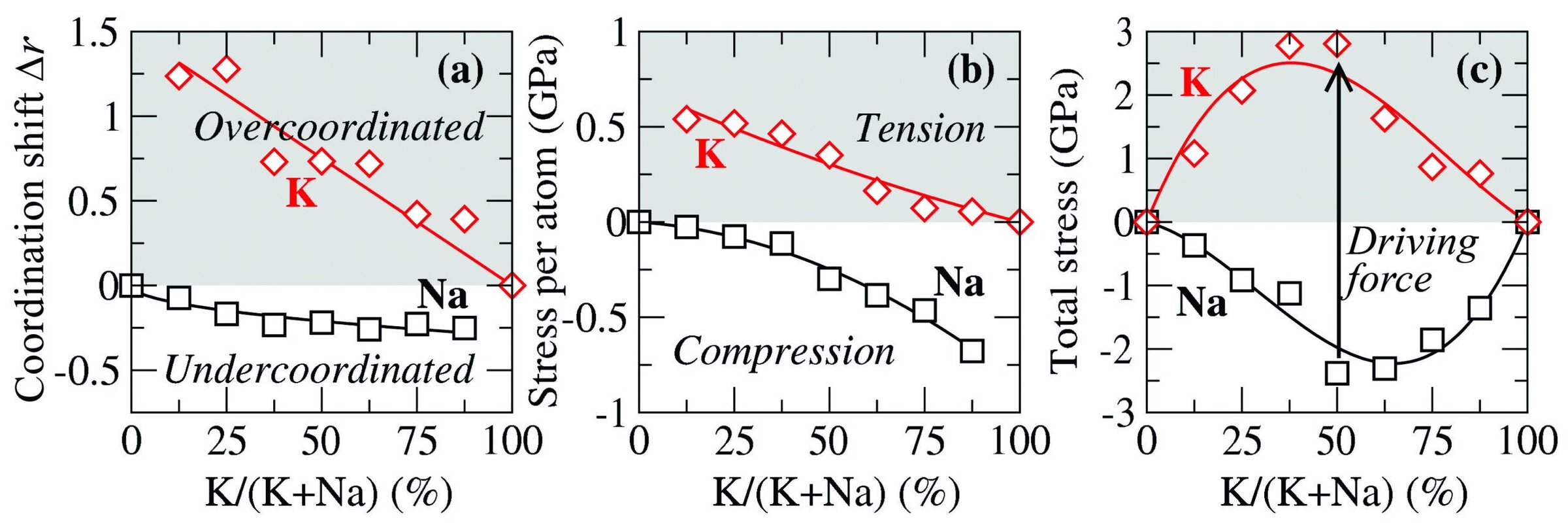
Figure 2. (a) Shift of the coordination number of sodium (potassium) atoms, using the binary sodium (potassium) silicate glass as a reference, with respect to composition of the glass. (b) Average stress per sodium and potassium atoms. A positive (negative) stress denotes local compression (tension). (c) Total cumulative stress experienced by all sodium and potassium atoms. Credit: Yingtian Yu

To assess this hypothesis, we first computed the coordination number of all atomic species. Figure 2(a) shows that the coordination number of sodium decreases upon addition of potassium, whereas that of potassium increases upon addition of sodium—which we attribute to mismatch between alkali atoms and the rest of the silicate network as we move away from the binary composition. This miscoordinated state forms local stresses inside the atomic network, which we assessed by computing the local stress applied to each atom.¹⁴ Figure 2(b) shows that the average stress experienced by sodium atoms increases upon addition of potassium, whereas that experienced by potassium atoms decreases upon addition of sodium.

We explain this as follows.

Overcoordinated potassium atoms present an excess of oxygen atoms in their first coordination shell. Because of mutual repulsion, oxygen atoms tend to separate from each other, which, in turn, tends to stretch the potassium–oxygen bonds. On the other hand, undercoordinated sodium atoms show a deficit of oxygen atoms, which, in turn, are more attracted by the central cation. This results in compression of sodium–oxygen bonds.

We then explain the mechanism of glass relaxation as follows.

Miscoordinated species act as local instabilities (or “excitations” following Phillips terminology). These excitations diffuse via local deformations of the atomic network, until an atomic arrangement that is locally under compression meets one that is under tension. At this point, both excitations are annihilated (or reach a “trap”), thereby relieving initial internal stress stored in the network.

The driving force for relaxation corresponds to the difference between total cumulative stress experienced by sodium and potassium atoms, which results from the balance between two competitive behaviors. In the first behavior, absolute stress per atom experienced by sodium and potassium species increases upon addition of potassium and sodium, respectively. In contrast, in the second behavior, numbers of sodium and potassium atoms present in the network decrease upon their replacement by potassium and sodium atoms, respectively. Altogether, total cumulative stress experienced by sodium and potassium atoms reaches a maximum when the number of sodium atoms equals the number of potassium atoms (Figure 2(c)). This behavior provides an intuitive atomistic origin of the excessive volume relaxation of glasses comprising mixed alkali atoms (i.e., thermometer effect).

In future work, we plan to extend analyses to mixed-alkaline-earth silicate glasses to assess the generality of these results. Besides relaxation, we also plan to investigate the effect of local atomic instabilities evidenced herein on the mechanical properties of glasses.

Acknowledgements

This work was supported by the National Science Foundation under Grant No. 1562066 and Corning Incorporated.

Editor’s note

Yu will present the 2017 Kreidl Award Lecture at the Glass and Optical Materials Division Annual Meeting, during the Pacific Rim Conference on Ceramic and Glass Technology, in Waikaloa, Hawaii, on May 24, 2017.