Throughout humanity, materials have defined the ages: Access to new materials creates novel paradigms for tool design.
One of the most engineered materials today is steel, with concrete and aluminum being close behind. Our understanding of steel process–structure–property relationships is so advanced that we can design new formulations predominantly from computation (with a few experiments for validation and tuning). Examples of steel products designed this way by QuesTek include Ferrium C61 for automotive applications,1 Ferrium C64 for rotor blades,2 and Ferrium M54 for airplane landing gears,3 among others.
If we can design steel predominantly from computation, then can we use the same principles to address the needs of ultrahigh-temperature materials for the leading edges of next-generation reentry vehicles? While the answer is “yes” theoretically, currently we do not have the necessary data for this approach.
According to “Digital Science – Dimensions,”4 there are about 6,500,000 publications on steel, with the oldest in the database dating back to 1665. By comparison, there are only about 27,000 publications on a key hypersonic material, zirconium diboride (ZrB2), with the oldest in the database dating back to 1905. While it is clear that Digital Science is missing some of humanity’s knowledge on steels and ZrB2, as humans have been working with steel and iron–carbon derivates since the Roman era and before,5 it still highlights that our understanding of steel is vast in comparison to ultrahigh-temperature materials.
For the development of future material systems such as ZrB2 and its composites, we must increase our comparative knowledge of ultrahigh-temperature materials. Statistical tools can help researchers design targeted experiments that increase the amount of data on these materials in a cost-effective and rapid manner. But first we must quantify the uncertainty of existing data so frameworks can be built that reduce uncertainty, thus allowing new materials systems to be developed more reliably.
The need to develop new tools for uncertainty quantification led researchers to organize the “Uncertainty Quantification of Materials Processing for Ultrahigh-Temperature Materials” symposium session and a workshop at ACerS Annual Meeting at MS&T24 in Pittsburgh, Pa. The goal for this session and workshop was to bring together computational, mathematical, and experimental experts to discuss several topics: (i) state-of-the-art uncertainty quantification, (ii) database development, (iii) statistics in data-poor regimes, and (iv) robust microstructure descriptors. These discussions were incorporated into the workshop designed for undergraduate and graduate-level students, which welcomed about 20 participants, and the symposium session targeted at researchers and professors, which attracted about 80 attendees.
This article provides a snapshot of the workshop and the symposium session along with our perspective on the current state-of-the-art uncertainty quantification methods, limitations and next steps to improve these methods, and commentary on the development of a ZrB2 process–structure–property database. In particular, the article highlights two presenters whose work is at the nexus of these challenges: Noah Paulson at Argonne National Laboratory, who discussed Bayesian methods in computational thermodynamics, and Jeremy Mason at the University of California, Davis, who discussed microstructure classification and the microstructure state space.
Workshop overview
The workshop began with an overview of hypersonic platforms, including the origins of aerodynamic heating and a brief history of hypersonic materials.6 The role of ZrB2 as a matrix material for next-generation ceramic matrix composites was then discussed, which led into discussion of an in-development process–structure–property database for ZrB2 that currently contains 82 publications from 1950–2024 (~143 data entries).
Three key insights stand out when reviewing this database. The first is that chemical composition is the least populated of the entries. This finding means that, in general, impurities in ZrB2 have not been well characterized, which highlights the importance of having statistical tools to help handle the uncertainty in ZrB2 impurities and their resulting effects on properties. The second is that 2D microstructure entries are well populated while 3D microstructure characterization is rare. 3D microstructure characterization is difficult but will be required to understand microstructure evolution and failure mechanisms, especially when expanding to ceramic matrix composites. The third is that properties are clustered, i.e., samples are measured for a single property, such as thermal conductivity or flexural strength, but rarely characterized for multiple properties on the same sample. This finding highlights the need for more diverse materials characterization studies to build statistics.
From these insights, the workshop discussion then turned to statistical tools that can be implemented in data-limited regimes. Two core statistical/machine learning techniques were discussed: (i) multifidelity surrogate modeling and (ii) matrix completion. Surrogate modeling involves developing a complex mathematical model to describe the behavior of a complex system. This technique is widely used in materials science and engineering for applications such as optimization, digital twins, and uncertainty quantification. On the other hand, matrix completion involves estimating missing entries in a matrix based on the available data. This technique has a wide range of applications in materials science and engineering, such as predicating unreported or unmeasured quantities and supporting surrogate modeling efforts.
Currently, many questions involving ultrahigh-temperature materials involve a large number of input variables with limited data. While matrix completion can help predict gaps in the data, there are still significant challenges to building surrogate models with such scarce data. To overcome this challenge, a multifidelity surrogate model was used at this workshop. This model used Gaussian process regression to combine high-fidelity, scarce-labeled data with many low-fidelity samples to minimize the need for high-fidelity labeled data points.
While this approach minimizes the need for high-fidelity data, comprehensive data collection is still a crucial part of reliable uncertainty quantification. Storing the collected data in a structured manner that can be retrieved easily—along with advanced search capabilities to screen through them—is beneficial. Making the collected data freely available would encourage sharing among different users in the scientific community as well.
For this purpose, the workshop introduced the National Institute of Technology’s Materials Data Curation System (MDCS),7 which is developed within the broader Configurable Data Curation System (CDCS).8 CDCS is a family of systems for structuring, searching, and sharing data based on extensible markup language (XML). XML is utilized as it is a robust, proven standard written as plain text and can be shared and converted into other formats easily. The purpose of MDCS and CDCS is to (i) increase the availability and quality of scientific data for higher community standards, (ii) increase the integration of scientific data among different platforms for federated searches, and (iii) support the development of FAIR (Findable, Accessible, Interoperable, Reusable) data communities.
Symposium session overview
The symposium session presentations were categorized into three broad themes: (i) uncertainty quantification of thermochemical data, (ii) uncertainty quantification of microstructural data, and (iii) applications of uncertainty quantification in ultrahigh-temperature material systems.
Discussions on thermochemical data were led by Noah Paulson (Argonne National Laboratory), Theresa Davey (Bangor University), and Raymundo Arroyave (Texas A&M). Current research efforts in this area involve developing protocols that use Bayesian methods for uncertainty quantification (UQ) and uncertainty propagation (UP) within the CALPHAD (CALculation of PHAse Diagrams) framework. These methodologies address the intrinsic uncertainties present in experimental data and model parameters, which significantly influence the reliability of predictions. By explicitly accounting for these uncertainties, UQ and UP enable more accurate and robust decision-making in materials design and optimization. Regarding the in-development ZrB2 database, these UQ and UP methodologies will help address the sparsity in chemical composition and will help identify optimum experimental plans to remedy this challenge.
Discussions on microstructural data were led by Jeremy Mason (University of California, Davis). Historically, microstructures have been characterized based on features defined from human observations. With the advent of computers and statistics, new and more objective metrics for defining microstructures are being proposed.
For example, new methods involve breaking down material microstructures into smaller regions or “windows.” Conceptually, materials can be compared by sampling many windows from each microstructure and finding the best possible matching between the two window sets. While two materials with identical processing conditions will not have identical microstructures, it is very likely that the windows in one set could be matched with similar windows in the other set. Notably, this matching ability is not true for materials with different processing conditions. This idea can be formalized by defining an underlying probability distribution of windows that would be sampled from random locations for each microstructure and then comparing the probability distributions of windows for two materials of interest.
Regarding the in-development ZrB2 database, these novel microstructure characterization techniques well help better characterize and understand uncertainty within the already existing microstructures, thus allowing for more precise development of new microstructures. In addition, it will assist in the analysis of more complicated 3D microstructures.
In terms of ultrahigh-temperature material systems, a variety of statistical tools can be applied to high-temperature material manufacturing challenges. Tenfei Luo of the University of Notre Dame presented a probabilistic physics-integrated neural differential modeling framework for accurately predicting outcomes of the isothermal chemical vapor infiltration process,9 a complex manufacturing method essential for producing high-temperature-resistant carbon composite materials.10,11 Meanwhile, Soumya Sirdar of the University of Pittsburgh presented a CALPHAD model to predict the effective thermal conductivity, including porosity and impurities for ZrB2.
Highlighted presenters
Bayesian methods in computational thermodynamics
Noah Paulson, Argonne National Laboratory

Noah Paulson, Argonne National Laboratory
Computational thermodynamics is an essential tool in the design and deployment of materials for extreme environments. However, while CALPHAD databases span an enormous compositional space, data is sparse, which leads to potentially unreliable predictions for multicomponent materials.
In recent years, researchers have prioritized the development of uncertainty quantification approaches for CALPHAD modeling to provide useful uncertainties. At Argonne National Laboratory, we have explored the potential of Bayesian methods for uncertainty quantification, with particular attention to parameter inference, uncertainty quantification and propagation (UQ&P), and automated dataset weighting.
Bayes theorem describes how the probability distribution of a model’s parameters, contingent on observed data, is proportional to the data likelihood, which describes the probability of observing data in the context of a specific model and its associated parameters, and the prior distribution, which describes the probability distribution of the model parameters before observing the data. The probability distribution is typically specified via mathematical or physical constraints and expert insights. Marginalizing the data likelihood and prior distributions over the entire parameter space yields the marginal likelihood, which describes the probability of the data given a choice of model.
For two models with equal prior probabilities of describing anticipated data observations, the ratio of marginal likelihoods (i.e., the Bayes’ Factor) expresses the Bayesian degree of preference for one model over another. Analytical solutions for the posterior are not tractable for many choices of model, data likelihood, and prior distribution. Consequently, we have turned to approximate Monte Carlo inference methods, which also enable efficient estimation of the marginal likelihood.
The discrete nature of the posterior representation obtained from these Monte Carlo methods lends itself to numerical uncertainty propagation. In this case, uncertainty intervals on the model prediction are obtained by evaluating the model on a representative sample of parameter sets from the converged posterior distribution; percentile bounds are then calculated on these sampled model predictions. In the paper by Low et al.,12 we employed these approximate methods to develop thermodynamic descriptions of monoclinic and tetragonal HfO2 from 0 up to 3000 K based on first principles calculations.
Careful specification of the data likelihood and prior distributions enable diverse modeling capabilities. For example, in Paulson et al.,13 instead of directly employing reported uncertainties for experimental datasets in the likelihood definition, the uncertainties were treated as potentially inaccurate. So, they were rescaled with a per-dataset hyperparameter that was included in the inference procedure alongside the model parameters.
This simple modification to the likelihood definition enabled more robust model selection, parameter inference, and UQ&P by giving the model the freedom to identify dataset weightings. This robustness led to thermodynamic consistency across specific heat and enthalpy measurements for elemental hafnium, and in the paper by Gabriel et al.,14 for aluminum considering both atomistic and experimental datasets.
Bayesian methods were also explored for binary systems with two distinct species. In the work by Paulson et al.,15 the open-source ESPEI python package16 was leveraged to perform Bayesian inference for the copper–magnesium binary system. As illustrated in Figure 1, this approach involved first identifying inferable parameters from the traditional database file, then performing numerical Bayesian inference via ESPEI, and finally performing UQ&P analyses for standard CALPHAD prediction outputs.
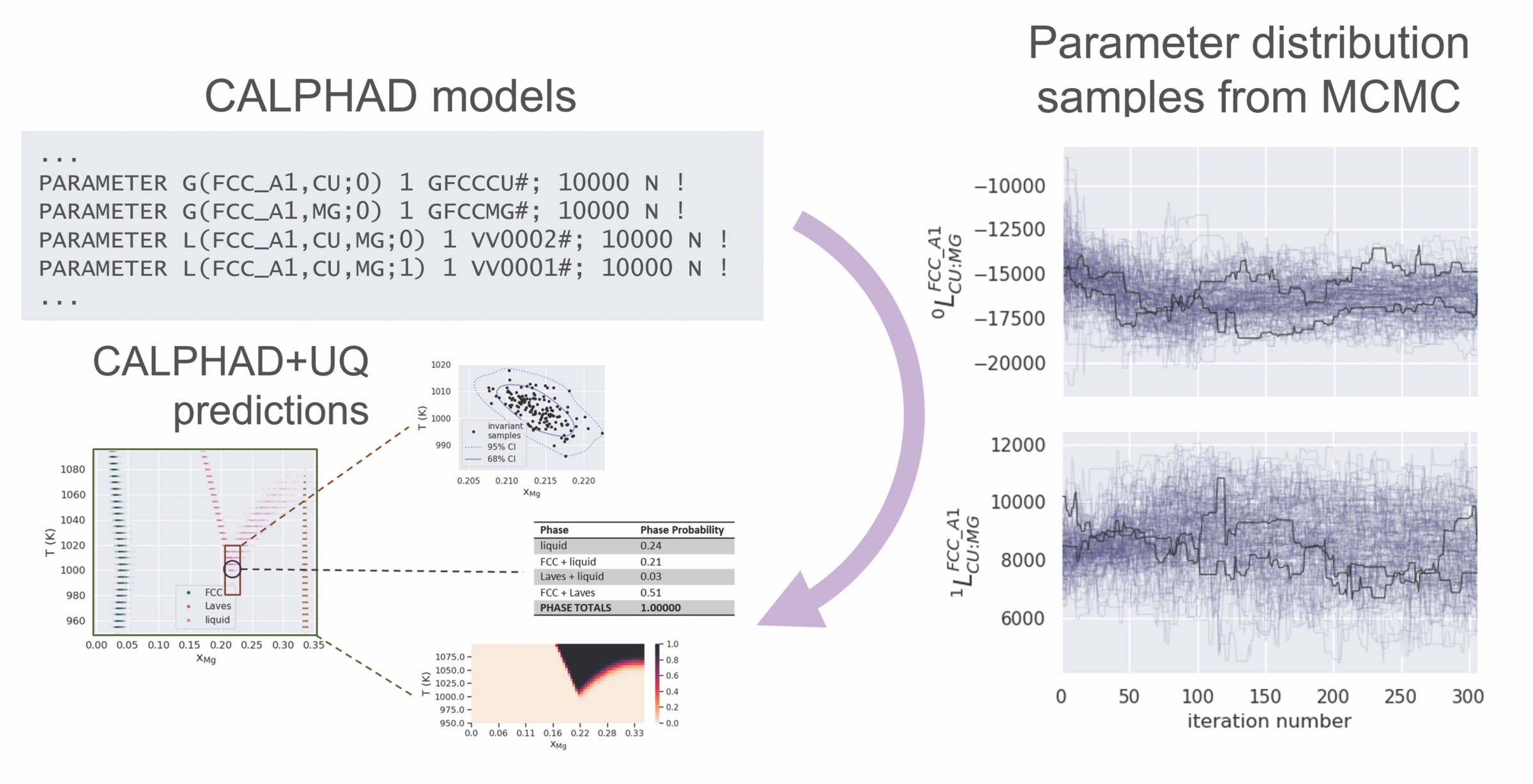
Figure 1. Schematic representation of Bayesian inference in CALPHAD for the copper–magnesium (Cu–Mg) binary thermodynamic description, which leads to UQ&P capabilities spanning those common in deterministic CALPHAD methods. Adapted from Reference 14. Credit: Noah Paulson
The novelty of this work was in the final stage, where the previously described numerical uncertainty propagation approaches were applied to diverse CALPHAD predictions, including the base thermodynamic quantities, the overall phase diagram, invariant points, and phase fractions at any composition, temperature, and pressure.
Most recently,17 we explored a question at the core of CALPHAD—how can we efficiently propagate uncertainties from unary systems to binary systems and beyond? The simplest approach would be to include the parameters for the thermodynamic descriptions of the individual species alongside the parameters of the binary phase descriptions. Unfortunately, this approach would not scale to practical thermodynamic databases with dozens of species and potentially thousands of parameters due to the computational limitations of numerical Bayesian inference.
Instead, we proposed performing inference on the thermodynamic descriptions of the individual species first and then numerically propagating these uncertainties during inference for the parameters of the binary phases. While phase diagrams and uncertainties were not identical between these two approaches for the copper–magnesium system, the results were comparable, indicating that this propagation approach was worth further investigation.
The ultimate goal of our work is to enable UQ&P for multicomponent thermodynamic databases, in turn enabling accelerated materials development and deployment. In a 2023 workshop, we examined three core areas of development required to reach this goal: (i) improving access to data and models, (ii) core UQ&P methodology development, and (iii) automated tools to aid CALPHAD assessment. Ultimately, progress in CALPHAD will inspire progress in the greater materials science field.
Microstructure classification and the microstructure state space
Jeremy Mason, University of California, Davis

Jeremy Mason, University of California, Davis
Advances in processing methods enable increased control of material microstructures and thereby material properties. Consequently, the development of integrated computational materials engineering (ICME)18 systems requires a canonical description of material microstructures. The ideal microstructure state space for ICME systems would have the following properties:
- Any microstructure can be represented as a point in the state space.
- The state space specifies enough microstructural information to constrain the material properties.
- Increasing the statistical similarity of two microstructures reduces the distance between the corresponding points in the state space.
The availability of such a microstructure state space would have widespread and significant implications for materials science. For example, material standards could be defined by means of the similarity of a produced microstructure to a reference one, thus allowing manufacturers to use any processing procedure provided the microstructure conforms to the specification. Furthermore, a materials database constructed on this state space could allow the properties of a proposed material to be interpolated by a distance-weighted average of properties of known materials. Processing routes to an arbitrary target microstructure could then be realized by an automated iterative process in which the next processing step is selected to most rapidly reduce the distance to the target microstructure.
Establishing such a microstructure state space is difficult, however. Regarding the first property, that any microstructure can be represented as a point in the state space, one subtlety is that many instances of nominally equivalent microstructures (e.g., all microstructures produced by a standardized processing procedure) should be identified with the same point up to statistical error. This decision requires a microstructure to be described as a probability distribution of small volume elements or “windows” at a user-specified length scale, effectively associating the material with a statistical volume element (SVE) that can be used to predict the material properties.19
The second property, that enough microstructural information be specified to usefully constrain material properties, requires that the representation of the SVE be explicit enough to allow property predictions. The SVE is fundamentally a probability distribution defined on a space that contains all possible windows. Given a distance function or other metric on the window space, the SVE can be approximated by a point cloud of windows sampled from experimental micrographs. The heterogeneity of such data means that the metric on the window space should be flexible enough to allow users to specify precisely what window features should be compared.
The third property relates to the measurement of distances on the microstructure state space. Given that points on the state space define microstructures as window distributions, the desired metric is a function that measures the similarity of probability distributions on the window space. Of the many metrics that are suitable for this purpose and are already available in the literature, the Wasserstein metric effectively reduces to finding the best match between two populations of sampled windows, where the cost of matching a single pair of windows is equivalent to the distance between them on the window space.20
Figure 2 visually represents these ideas. Two micrographs of material microstructures appear on the bottom row, with windows of a consistent size sampled uniformly at random from the interiors of the micrographs. The windows are represented as points in the window space on the middle row, with the points distributed according to underlying probability distributions μ and ν. Distances between points in the window space are measured by a function D that quantifies the similarity of the corresponding windows. The window distributions are represented as two points in the microstructure state space on the top row. Distances between points in the state space are measured by the Wasserstein metric W(μ,ν|D), which quantifies the similarity of the corresponding window distributions given the window metric D. That is, the statistical similarity of the two microstructures on the bottom row at the length scale of the windows is quantified by the distance between the corresponding points in the microstructure state space on the top row.
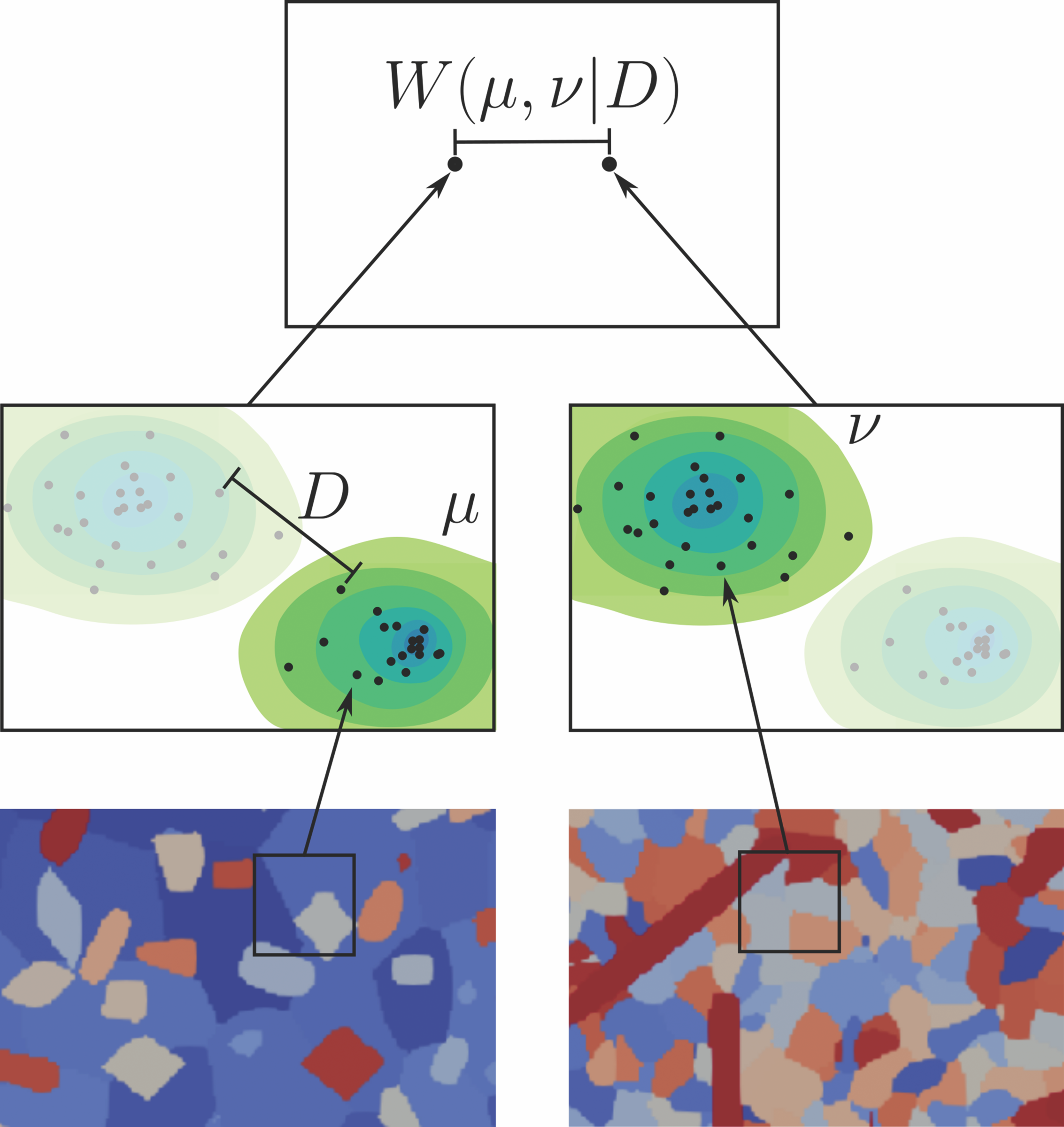
Figure 2. Schematic showing the various concepts involved in the construction of the microstructure state space. Credit: Jeremy Mason
In a preprint,21 we verified that such an approach is indeed possible for the restricted case of single-phase polycrystalline materials (or for general polycrystalline materials where only grain boundary geometry information is retained). One metric that allows the similarity of windows to be quantified is defined, and practical guidelines for the size of sampled windows, the number of sampled windows, and the area of the micrograph from which to sample are established. Pairwise distances are evaluated for a set of synthetic microstructures generated by the modeling software DREAM.3D, and a proof-of-concept microstructure database is constructed with a query capability whose computational cost is manageable. These efforts are not intended to be authoritative but merely to show that the vision described here could be realized in practice.
Conclusions
From the workshop and symposium session, it is clear that uncertainty quantification in materials processing for ultrahigh-temperature materials is an up-and-coming field that will grow in the future. Key areas will include the development of Bayesian methods for uncertainty quantification and uncertainty propagation in thermochemical data along with the CALPHAD method. These developments will be essential to understand where the next thermochemical measurements are required to effectively develop multicomponent elemental systems.
In addition, new statistical techniques to analyze microstructures, such as the microstructure state space, will be essential in quantifying the similarities and differences between two sets of microstructures. This ability will be critical to reduce uncertainty in materials whose properties are highly sensitive to microstructure, such as ceramics and other brittle systems.
Finally, novel statistical methods that can be applied in data-poor regimes will be essential in pushing the boundaries in new and emerging material systems. These ideas will enable new material technologies, such as ZrB2 and its subsequent composites, to catch up much faster to the maturity of established systems, such as steel.
Future conferences
In 2026, the “Uncertainty Quantification of Materials Processing for Ultrahigh-Temperature Materials” session will expand to become a full symposium at MS&T26 in Pittsburgh, Pa.
Acknowledgments
The authors would like to acknowledge the workshop presenters and the session presenters for their contributions in enabling a successful meeting. In addition, the authors would like to thank Bai Cui at the University of Nebraska for allowing us to pair this session with his “Manufacturing and Processing of Advanced Ceramic Materials” symposium at MS&T24.
The workshop presenters include Scott J. McCormack (University of California, Davis) Soumya Sridar (University of Pittsburgh), and Hessam Babaee (University of Pittsburgh). The symposium session presenters include Noah Paulson (Argonne National Laboratory), Jeremy Mason (University of California, Davis), Tenfei Luo (University of Notre Dame), Raymundo Arroyave (Texas A&M), Theresa Davey (Bangor University), and Soumya Sridar (University of Pittsburgh).
We also want to acknowledge support from the Air Force Office of Scientific Research, Aerospace Composite Materials portfolio (program manager Derek Barbee) under contract number FA9550-24-1-0309.
Cite this article
S. Sridar, W. Xiong, H. Babaee, W. Fahrenholtz, and S. J. McCormack, “Uncertainty quantification of materials processing for ultrahigh-temperature materials,” Am. Ceram. Soc. Bull. 2025, 104(2): 28–33.
About the Author(s)
Soumya Sridar is a visiting research assistant professor at the University of Pittsburgh. Wei Xiong and Hessam Babaee are associate professors at the University of Pittsburgh. William Fahrenholtz is professor at Missouri University of Science and Technology. Scott J. McCormack is assistant professor at the University of California, Davis. Contact McCormack at sjmccormack@ucdavis.edu.
Issue
Category
- Refractory ceramics
Article References
1Wright J. A., Sebastian J. T., Kern C. P., and Kooy R. J., “Design, development, and application of new, high-performance gear steels,” Gear Technology 2010, 27(1): 46–53.
2Wright J.A. and Sebastian J., “Secondary-hardening gear steel,” U.S. Patent 8801872B2 (2008).
3H.-J. Jou, “Lower-cost, ultra-high-strength, high-toughness steel,” U.S. Patent 20160376686 (2009).
4“Digital Science – Dimensions.” Searched 30 Jan. 2025 for the key terms “steel” and “zirconium diboride OR zirconium di-boride OR ZrB2.”
5Lang J., “Roman iron and steel: A review,” Materials and Manufacturing Processes 2017, 32(7–8): 857–866.
6Peters A. B., Zhang D., Chen S., et al. “Materials design for hypersonics,” Nat Commun. 2024, 15(1): 3328.
7“Materials Data Curation System,” National Institute of Standards and Technology.
8“Configurable Data Curation System,” National Institute of Standards and Technology.
9Akhare D., Luo T., and Wang J.-X., “Physics-integrated neural differentiable (PiNDiff) model for composites manufacturing,” Comput. Methods Appl. Mech. Eng. 2023, 406: 115902.
10Akhare D., Chen Z., Gulotty R., Luo T., and Wang J.-X., “Probabilistic physics-integrated neural differentiable modeling for isothermal chemical vapor infiltration process,” npj Comput. Mater. 2024, 10(1): 120.
11Akhare D., Luo T., and Wang J.-X., “DiffHybrid-UQ: Uncertainty quantification for differentiable hybrid neural modeling.” arXiv 2023.
12Low J. J., Paulson N. H., D’Mello M., and Stan M. “Thermodynamics of monoclinic and tetragonal hafnium dioxide (HfO2) at ambient pressure,” Calphad 2021, 72: 102210.
13Paulson N. H., Jennings E., and Stan M., “Bayesian strategies for uncertainty quantification of the thermodynamic properties of materials,” Int. J. Eng. Sci. 2019, 142: 74–93.
14Gabriel J. J., Paulson N. H., Duong T. C., et al. “Bayesian automated weighting of aggregated DFT, MD, and experimental data for candidate thermodynamic models of aluminum with uncertainty quantification,” Materialia 2021, 20: 101216.
15Paulson N. H., Bocklund B. J., Otis R. A., Liu Z.-K., and Stan M., “Quantified uncertainty in thermodynamic modeling for materials design,” Acta. Mater. 2019, 174: 9–15.
16Bocklund B., Otis R., Egorov A., Obaied A., Roslyakova I., and Liu Z.-K., “ESPEI for efficient thermodynamic database development, modification, and uncertainty quantification: application to Cu–Mg,” MRS Commun. 2019, 9(2): 618–627.
17Gabriel J. J. and Paulson N. H., “Uncertainty propagation of unary components for the Bayesian inference of n-nary phase diagrams: Example of Cu–Mg,” SSRN 2023.
18National Research Council, Integrated Computational Materials Engineering: A Transformational Discipline for Improved Competitiveness and National Security. Washington, D.C.: National Academies Press, 2008.
19Ostoja-Starzewski M., “Material spatial randomness: From statistical to representative volume element,” Probabilistic Engineering Mechanics. 2006, 21(2): 112–132.
20Villani C., Optimal Transport. Berlin, Heidelberg: Springer Berlin Heidelberg, 2009.
21Miley D., Suwandi E., Schweinhart B., and Mason J., “A metric on the polycrystalline microstructure state space,” arXiv 2024.
Related Articles
Bulletin Features
Optical-grade ceramics: Historical turning point for the design of optical elements
When observing the microstructure of ceramics, researchers frequently see residual pores and structural defects, such as segregation at grain boundaries. These defects serve as scattering sources of incoming light, which affect the optical properties of ceramics and make them inferior to single crystals in optical applications. But what if these…
Bulletin Features
With safety and performance, ceramic batteries are in the works
Governments around the world are pouring funding and resources into building up renewable energy infrastructure to reduce reliance on greenhouse-gas-emitting fuels. However, relying solely on wind and solar power is challenged by the fact these technologies cannot provide a reliable baseload, which is the constant minimum flow of energy required…
Bulletin Features
Glassy solid-state electrolytes for all-solid-state batteries
The introduction of the lithium-ion battery (LIB) to the market in 1991 revolutionized the energy storage field and enabled the development of portable electronic devices and electric vehicles that are widely available today. The improved energy density and cycle life compared to previous rechargeable batteries, such as lead-acid or nickel-metal-hydride,…





